The media is buzzing with excitement over last week’s NCEA Level 1 MCAT (Mathematics Common Assessment Task) examination. Students are in tears and teachers are outraged over the exam that was “very different in style” and “far too difficult”.
For those who don’t know what the MCAT is, or why the MCAT might be so important, here are some salient facts:
- The examination topic is algebra, specifically “Apply algebraic procedures in solving problems”.
- This is an external NZQA exam, administered internally by the high schools in September. Prior to 2011, algebra was examined in November, as part of the three-hour end-of-year external exam.
- Calculators are NOT allowed in this examination.
- Schools may struggle to administer the exam in a single day, so there are two similar, but different, versions of the exam – one to be delivered on a Tuesday, the other on a Thursday.
- The traditional assessment (as opposed to the trial online EMCAT) was made harder last year. From the official NZQA assessment (marking) schedule: “The style of some of the questions in this year’s assessment has changed so as to align more closely with the requirements of the achievement standard. The title of the standard requires the candidate to use algebraic procedures in solving problems.”
- Students who don’t do well in algebra at NCEA Level 1 will have limited options at NCEA Level 2. Such students are typically not allowed to study calculus at Level 2.
- Students who don’t do well in algebra will struggle with calculus.
- Students who don’t do well in algebra or calculus will find it difficult to pursue STEM subjects at university.
So just how different or difficult was the exam? Now that the papers are in the public domain, I will review one of them (the Thursday paper) here. If you aren’t interested in the details, you can skip to the conclusion here.
[Update: I have seen the assessment (marking) schedule and added comments below. As with most NCEA exams, it’s not the questions I have so much of a problem with, it’s how they are assessed…]

The intention here is probably for students to factorise the quadratic as  and supply the two factors as the side lengths. However, I suspect the examination team failed to notice that this question has infinitely many possible answers. For example, another factorisation that students might have reasonably obtained is
and supply the two factors as the side lengths. However, I suspect the examination team failed to notice that this question has infinitely many possible answers. For example, another factorisation that students might have reasonably obtained is

The wording of this question should have been sharpened so that the intended factorisation (if there was one) was made clear. (See Question Three (a)(i) below.)
[Update: As predicted, the assessment schedule does not allow for any answer other than the intended factorisation. I pity anyone who offered a different but valid answer.]
Poor wording aside, factorising quadratics is a basic algebraic procedure that is typically introduced to Year 10 students, and this question put a thin veneer of an application on top. Level 1 students should be familiar with applying algebra in the context of measuring area, albeit in the opposite direction. If they knew how to multiply two quantities to form the area of a rectangle, it doesn’t seem unreasonable to expect them to recognise that this question was asking them to reverse that process.

This is a reasonable question. Students at this level should be able to solve a quadratic equation that is not equal to zero to begin with, but can be made equal to zero and then factorised.
[Update: To my surprise, if this question was answered in full, it was worth an Excellence! That should cheer up a few people.]

This is a simultaneous equations question, not trivial, but reasonable.
[Update: If students were able to write down at least one equation correctly, that was worth an Achieved.]

This is a basic procedure, namely adding algebraic fractions. There is hardly anything to do here – they even supply the answer. The subtraction of algebraic fractions appears more commonly in maths exams because students are frequently caught out by multiplication of negative numbers.

This is probably one of the questions that some people are suggesting is more suitable for NCEA Level 2. I am inclined to disagree. Certainly, a general index equation might require logarithms to solve it, but not this one. As long as students recognise that  , this question is manageable.
, this question is manageable.
Furthermore, this index question is not much harder than index questions in previous years. Last year’s trial online EMCAT asked “What is the connection between  and
and  if
if  ?” Again, as long as students know that
?” Again, as long as students know that  , they should be able to say something sensible. In the 2014 MCAT, students were asked to solve
, they should be able to say something sensible. In the 2014 MCAT, students were asked to solve  .
.
In summary, I feel that Question One is fair. Part (a)(i) might have deviated from early questions in past papers of the “Factorise this” or “Simplify that” variety, but the application was not particularly difficult or surprising. As NZQA pointed out last year, the title of the standard is “Apply algebraic procedures in solving problems”.

This question is an algebraic substitution question. The fact that the equation modelled a parabola is again a thin veneer of an application. If students didn’t know what a parabola was, I hope they managed to ignore it and press on.

Solving algebraic inequalities seems to unsettle students, even though the steps required are almost identical to the steps required to solve algebraic equations – there is only one extra thing to remember, which is to reverse the inequality if multiplying or dividing by a negative number. All steps required to solve this question should be known to students at this level. [Update: Even just one correct expansion was worth an Achieved.]
Interestingly, this was one of the few occasions where the parallel question in the Tuesday paper was noticeably trickier at first appearance, because there were identical factors on both sides of the inequality and it might have been tempting to cancel them out. Unfortunately, that would have led to something nonsensical. The lack of equivalence between these parallel questions is something that should have been picked up by the examination team and corrected.

This is potentially another question that looks like a Level 2 question, but isn’t. A reasonable first attempt at solving this would be to rewrite the inequality as  . A sharp observer might notice that
. A sharp observer might notice that



Either way, as long as students know their powers of 2 up to 32, they should see that the whole number  has to be less than or equal to 5. As noted above, index questions of this type have been asked in previous years. Changing an equality symbol to an inequality symbol does not affect the algebra required to solve the problem.
has to be less than or equal to 5. As noted above, index questions of this type have been asked in previous years. Changing an equality symbol to an inequality symbol does not affect the algebra required to solve the problem.

This question requires students to expand and simplify two expressions and then look for similarities between them. If students had seen a similar 2014 MCAT question, in which students were asked to write  in terms of
in terms of  , then they would have been adequately prepared to attempt this question. [Update: Even just one correct expansion was worth an Achieved.]
, then they would have been adequately prepared to attempt this question. [Update: Even just one correct expansion was worth an Achieved.]

OK, this is where things start to get interesting! Students were given 9 lines of paper in which to conduct their investigation and answer this part of the question.
Firstly, what is meant by “when Janine changes the order of the numbers in Line 1”? The directness of the question “Does she get the same answer as in Line 4?” suggests that we are supposed to investigate a single event. But there are 23 ways in which Janine could change the order of the numbers. Are students expected to try all 23 ways? Over 9 lines of paper, probably not. If we are meant to infer that Janine changes the numbers only once, how can we possibly investigate if we don’t know what the new order looks like? The wording of the question is decidedly murky.
In actual fact, the answer is “yes” or “no”, depending on how the numbers are re-ordered. I’ve seen probability questions in which a “yes” is an Achieved answer but a “no” is a Merit answer, but at this early stage in this question, students would be choosing a new order at random, so it would be unfair if either answer fell into a different achievement band.
[Update: If you tried one rearrangement and said “yes” or “no”, that was worth an Achieved. So even though I understood the question well enough to perform a succinct investigation with the preferable answer of “no”, I would have only gotten an Achieved. If you tried two rearrangements but didn’t say anything, that was also an Achieved. The wording of the Merit criteria is just as nonsensical as the question, but I think they want at least two rearrangements with a point of difference and some sort of statement about one’s findings.]

I had to parse this sentence many times and came to the conclusion that it doesn’t make a lot of sense, even after tweaking it to read “Find, using algebra, the relationship between the numbers in Line 1 and the numbers in Line 4 when she changes the order of the numbers in Line 1.” If students are meant to investigate what happens to the expression for the number in Line 4 after the numbers are changed, then it has not been made very clear. A better question would be “Using algebra, show how the number in Line 4 might be affected if Janine changes the order of the numbers in Line 1.”
This question doesn’t feel like problem solving. We are using algebra to make a general observation. Students at Level 1 will have very little experience of using algebra in this way, but such questions have been seen in other Level 1 Maths assessments in the past, namely “Tables, Equations and Graphs”, an end-of-year assessment concerned specifically with the application of algebra to graphs.
It is certainly possible to express the number in Line 4 in terms of the numbers in Line 1 at any given point in time. For example, if the numbers in Line 1 are called  , then the number in Line 4 is
, then the number in Line 4 is  . But perhaps we are supposed to pay attention to the pattern of the example numbers 2, 4, 6, 8 and call the numbers
. But perhaps we are supposed to pay attention to the pattern of the example numbers 2, 4, 6, 8 and call the numbers  ? Is this important or is this a distraction?
? Is this important or is this a distraction?
I would conjecture that a student would be better able to answer part (i) after answering part (ii). That is the whole point of algebra, after all. It enables us to see patterns in numbers, or at least understand better the patterns that we see, because the numbers themselves often get in the way. Assuming there is a pattern in the numbers in Line 1 gets in the way of truly understanding any pattern that might be observed in the triangular formation, and ideally we should not be distracted by this. So my preferred setting of the first two parts of Question Two would be split into three parts:
- Janine changed the order of the numbers in Line 1 and found that it changed the number in Line 4. What might Janine’s new ordering look like?
- Janine wonders whether changing the order of the numbers in Line 1 will always change the number in Line 4. Use algebra to find the relationship between arbitrary numbers in Line 1 and the resulting number in Line 4.
- Use your expression for the number in Line 4 to explain how Janine could change the order of the numbers in Line 1 but not change the number in Line 4.

If students were brave enough to attempt this question, hats off to them! I quite enjoyed this question myself, but only students with a good understanding of divisibility would understand how to interpret the algebra in this question. Furthermore, open questions such as “what do you know?” are only fair if the answers are marked “openly”. Unfortunately, that’s not the case with NCEA. They still have something specific in mind, answered to a greater (Excellence) or lesser (Achieved) extent, or somewhere in the middle (Merit). Therefore, students should reasonably expect to be given better guidance as to what is intended by the question. E.g. “If the number in Line 4 is divisible by 3, then identify the position of the number or numbers in Line 1 that are divisible by 3.”
My final comment about this question is the lack of continuity. In part (iii), we were to assume there was a pattern in the numbers in Line 1, but it wasn’t the pattern demonstrated at the start of the question. It appears that the 2, 4, 6, 8 pattern was a red herring, and the examination team should have chosen numbers that appeared to be more random.
In summary, Question Two was fair up to part (d). Part (e) was poorly written and too hard for Level 1.

This question is almost identical to Question One (a)(i) but it has an important difference. One of the side lengths is given, which means the intended factorisation of the quadratic expression for the area has been made clear. It begs the question, why was Question One (a)(i) even included??

Another open question! What’s wrong with “State any restrictions on the value of  for this rectangle”?
for this rectangle”?
[Update: This is amazing. If you answer the question correctly, you only get an Achieved. If you say something about the area or the side lengths, i.e. more than was asked for, you get a Merit! If they wanted commentary on the area or the side lengths, why didn’t they just say “Explain.” at the end?]

This is a “changing the subject of the formula” question, and there have always been questions of this type in previous years.

Er, what’s this question doing here? This is the sort of basic procedural question that would have been better placed as Question One (a)(i).

This is not a trivial question, but it is suitable for Level 1. However, it’s worth noting that the parallel question in the Tuesday paper resulted in a quadratic equation that was different enough to be inequivalent. The Tuesday students may have struggled more than the Thursday students. This should not have happened.
[Update: Sure enough, the Tuesday question must have been done very badly, because you could get Excellence even if you didn’t quite solve the equation! I’ve also heard reports of students (not ours!) getting caught up trying to calculate the square root of 8 without a calculator…]
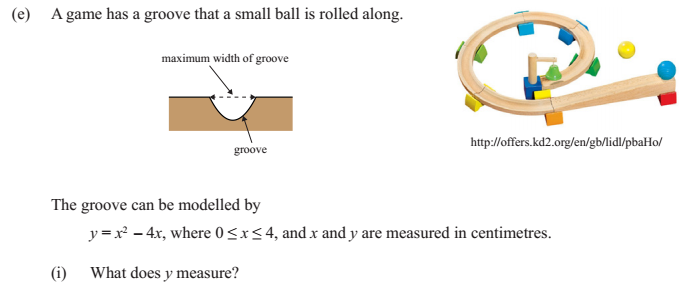
If students weren’t sure how to answer this question, looking at (ii) would have given them a good clue!

Like many NCEA questions, this is quite ‘wordy’ and requires a high level of literacy to understand the question. It also requires knowledge about the features of the graph of a quadratic expression, and the use of algebra to solve a quadratic equation. The icing on the cake is to form a percentage from the two quantities obtained (the maximum horizontal width and the width at a vertical depth of 3cm).
[Update: Solving the equation, i.e. bulk of the work and the algebraic heart of the problem, was only worth a Merit. The trivial step of calculating a numerical percentage at the end was what it took to get an Excellence. Seriously?? Where is the extended abstract thinking in there? I suspect the examination team pulled this question from a traditional “marks out of 100” paper but failed to modify it for NCEA.]
Although I think this is a reasonable Excellence question for this assessment, it is worth noting that this question could easily appear in the “Tables, Equations and Graphs” assessment at the end of the year. There needs to be some discussion about whether or not teachers and students should expect the same knowledge to be potentially assessed twice.
It seems that some schools had not yet taught their students about graphs, but in all fairness, last year’s MCAT exam had questions that required graphing knowledge.
In summary, Question Three was challenging but fair, provided students had been taught the appropriate material.
In conclusion…
This exam wasn’t a walk in the park, but actually most of the questions were fair for Level 1, even if they weren’t identical in form to past exam questions. There were certainly some poorly-worded questions, but unfortunately I see them in NCEA maths exams every year. MCAT 2016 is by no means the exception.
It is true that the MCAT now has fewer basic questions that test purely algebraic procedures, but most of these procedures should be introduced in Year 10, so it is not unreasonable to expect students be ready to apply them in Year 11. Given that the change in style occurred last year, I am surprised that the huge uproar didn’t occur 12 months ago.
Most importantly, I believe this year’s MCAT is the standard we should be aspiring to. Media reports suggest the reality in schools is very different. I will discuss this in my next post.
Dr Audrey Tan, Mathmo Consulting
20 September 2016
Regarding Q2e (given that this is algebra exam) (ignoring the awkwardness of the question wording)
my answer to both parts i and ii is to duplicate the diagram with the numbers in row 1 replaced with variables a,b,c,d, then row 2 is a+b b+c c+d
row3 is a+2b+c b+2c+d row4 is a + 3b + 3c + d. Now easy to say that swapping a and d or b and c makes no difference to the result, but swapping a and b or c and d does make a difference.
This isn’t hard algebra if you can figure out that this is what is wanted.
Part iii involves substituting a+1 a+2 a+3 for b,c,d in the above row4 a + 3a+3 + 3a+6 + a+3 = 4a+12
if 4a+12 is divisible by 3, this implies a is divisible by 3
LikeLike
oops, I missed the bit where you already said this. I agree the question part ii was worded terribly.
LikeLike
Last one on the same topic i promise. I think that jumping straight to part ii and getting the algebraic expression for arbitrary numbers gives a much more direct route to an answer than wooly “investigate” in part i
LikeLike
Agreed, and hence my suggested rewriting of parts (i) and (ii). Thanks for your posts.
LikeLike